lab06 : Nested Loops and Caesar Cipher

In this lab you’ll get to:

• Practice using nested loops
• Create encryption and decryption algorithms that use a secret key
• Write “helper” functions that are called by other functions
• Use built-in string methods
• Convert an integer to a binary representation (optional)

Lab06 Slides

You can view the accompanying slides to lab06 here.

Step 0: Get ready to start on this lab

• Log on and bring up a terminal window
• Create a directory in your cs8 directory named lab06. (Remember the commands cd, ls, and mkdir)
• Start IDLE
• Create a file lab06.py

Warm-Up functions (include these in your Gradescope submission)

1. Prime numbers

First, we will warm up with practicing nested for loop functions.

Create a list with all prime numbers between start and end (including start, if applicable, but not including end).

For example, to get a list of all prime numbers between 2 and 100, including the number two, we would call listPrimes(start, end). The output should be [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97].

Reminder: A prime number is a positive number that is evenly divisible (without a remainder) only by 1 and itself. One (i.e., the number 1) is specifically excluded from the list of primes in the definition.

• A prime number cannot be even, because all even numbers are divisible by 2: the only exception to this is 2 itself, because 2 “is evenly divisible (without a remainder) only by 1 and itself”.
• 9 and 15 are the first two odd numbers (other than the excluded 1), which are not prime, because they are divisible by 3.

First, draft a pseudocode for your approach (add it as comments in your file):

# Check that ...
# Check that ...
# Create ...
# For each number ...
#     If ...
#         TODO
# Return the list

Let’s try writing this function:

def listPrimes(start, end):
    """
    Return a list with all prime numbers 
    between `start` and `end` (including `start`, 
    if applicable, but not including `end`).
    Return None if start or end are not int
    or if they are less than or equal to 1.
    If no primes exist in the given range,
    return an empty list.
    """
    return "stub"

Now would be a good time to create a file lab06_tests.py and add the functions that test that your code is correct. One test is given to you above (a list of primes between 2 and 100), you can also test it with an invalid input or with simple cases, where the input (2, 3).

2. Matrix-scalar multiplication

Matrices are rectangular arrays of numbers like so:

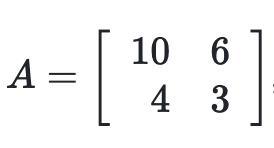
Another way to think about this would be a list of lists, where each list within the main list represents the values stored within one row of the matrix.

For example, the matrix from above could be written as:

A = [[10, 6], [4, 3]]

Like numbers, matrices can be multiplied by integers like so:

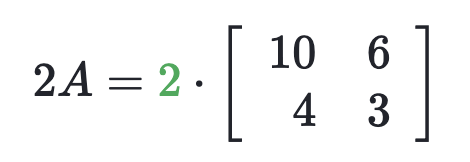
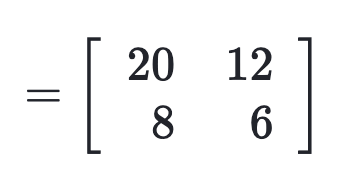
Write a function multiplyScalarMatrix() that simulates multiplying a matrix by a scalar value. This function takes two input parameters, one of type list which represents a matrix, and the other of type int which represents a scalar, and returns the product matrix in the form of a list.

For the example above, multiplyScalarMatrix([[10, 6], [4, 3]], 2) should return [[20, 12], [8, 6]].

Test it with another example: multiplyScalarMatrix([[6, 8], [10, 12]], 5) should return [[30, 40], [50, 60]].

Let’s look at yet another example, now testing it with a 2-by-3 matrix. multiplyScalarMatrix([[1, 5, 6], [2, 4, 6]], 3) should return [[3, 15, 18], [6, 12, 18]].

Think how you would approach the solution and draft a pseudocode for your approach (add it as comments in your file):

# Check that ...
# Check that ...
# Create ...
# For each number ...
#     ...
#         TODO
# Return the list

Time to check how well your pseudocode translatable into code.

def multiplyScalarMatrix(matrix1, scalar):
    """
    Input: matrix1 is a list, scalar is an integer.
    If incorrect input types are given, return None.
    Otherwise, return the list that represents
    a matrix that is the product of matrix1 and
    scalar.
    """
    return "stub"

Add a few tests to lab06_tests.py to verify that your function is behaving as expected.

3. Unscrambling tuple values by type

Ms. Frizzle has a list of tuples, one tuple for each student in her class. Each tuple contains the name of a student (type str), the perm number (of type int) of that student, and a boolean value to indicate whether the student was present that day (type bool). Unfortunately, each tuple got jumbled such that the name, perm number, and attendance status are not necessarily in that order. For example, one tuple is (True, 65473, 'Sarah'), and Ms. Frizzle would like it to read ['Sarah', 65473, True].

Help Ms. Frizzle write a function unscrambleTuples() that takes in a parameter list_of_tuples and returns a list of lists that stores the values in the way Ms.Frizzle wants: student’s name, student ID, attendance flag ([str, int, bool]).

For example, for a list that contains a single tuple, unscrambleTuples([(12345, False, 'Frodo')]) should return [['Frodo', 12345, False]].

Another example: unscrambleTuples([('Sarah', 65473, True), (True, 1234, 'Beyonce'), (False, 'Molly',2344)]) should return [['Sarah', 65473, True], ['Beyonce', 1234, True], ['Molly', 2344, False]].

As usual, think how you would approach the solution and draft a pseudocode for your approach (add it as comments in your file):

# Create ...
# For each ...
#     ...
#         TODO
# Return the list

IMPORTANT: When you create an empty list, you cannot directly index it, because it contains no elements. If you use append(), it adds elements to the end of the list, which might not be the order that you want. Sometimes, instead of an empty list, you can create a list with the paceholder (“stub”) values, which then gives you the ability to index (and change) those values directly.

def unscrambleTuples(list_of_tuples):
    """
    Given a list of tuples that contain values of type 
    string, int, and bool, unscramble the values to
    create a new list that turns each tuple from the
    list_of_tuples into a list with the values arranged
    by type as follows: [str, int, bool].
    """
    return "stub"

Add a few tests to lab06_tests.py to verify that your function is behaving as expected.

4. Custom range with user input

Write a function that uses the range() function and asks for a user input of "Enter a number between -100 and 100: " to control the range.

• If the number entered is less than 0, return a list with values starting at the given number to 0 with increments of 1.
• If the number entered is greater than 0, return that number to 100 with increments of 2.
• If 0 is entered, return 0.

def loop_function():
    """
    Ask for user input: 
    "Enter a number between -100 and 100: ". 
    If the number entered is less than 0, 
    return a list with values starting at 
    the given number to 0 with increments of 1. 
    If the number entered is greater than 0, 
    return that number to 100 with increments of 2. 
    If 0 is entered, return 0.
    """
    return "stub"

Caesar Cipher

Let’s finish the cryptography exercises that we started last week.

A Caesar cipher is one of the simplest and most widely known encryption algorithms. In this algorithm, each letter of the plaintext is replaced by a letter some fixed number of positions later in the alphabet. For example, with a shift number of 4, A would be replaced by E, B would become F, and so on.

Note that for this algorithm to work, the letters of the alphabet (and any other characters that should be allowed in the plaintext), as well as their order, must be fixed and should be the same for both encryption and decryption. For example, if you encrypt with the 26 letter English alphabet and decrypt with the 27 letter Spanish alphabet (including ñ), you won’t get the correct decrypted plaintext back.

Functions to Implement:

1. createAlphabet() - return alphabet * Note: This is the exact same as your function from lab05*
2. encryptCaesarCipher(plainText, key) - return cipherText
3. decryptCaesarCipher(cipherText, key) - return plainText

Function Details:

1) createAlphabet() - return alphabet. Note: This is the exact same as your function from lab05.

2) encryptCaesarCipher(plainText, key) - return cipherText. Write a function to perform encryption using the Caesar cipher. The first few lines of this function need to create your alphabet using the helper function createAlphabet() you created earlier.

You will have to use a for loop to go through the characters of your plaintext and for each character you will have to choose the character from the alphabet that is key positions forward in the alphabet. Be very careful for the cases where you will have to cycle around the ends of the alphabet. (Hint: You can use your getCharacterForward(char, key) from the previous lab.)

If the key is negative, you will have to choose the character from the alphabet that is key positions backward in the alphabet. Be very careful for the cases where you will have to cycle around the ends of the alphabet. (Hint: You can use your getCharacterBackward(char, key) from the previous lab.)

Do not hard-code any values in your code, use functions instead - we will be testing your code with the alphabets of different lengths.

3) decryptCaesarCipher(plainText, key) - return cipherText. Finally, write a function that decrypts the Caesar Cipher. Think: what process would you follow if you were doing the decryption by hand?

4) Test your functions by encrypting any string, and then decrypting the result to verify that you can recover the original input string. Try interesting test cases: short strings, long strings, strings with odd characters, large key values, creative key choices, etc.

Check your understanding: what happens if you first “decrypt” some plaintext, and then “encrypt” it? Why does this happen?

5) Decode this message with key = 247 to test that you are on the right track!

'RDCvGpIJApIxDCHjnjhDJjwpKtjuxCxHwtsjIwtjBpCspIDGNjEpGIjDujIwtjApql'

Save and Submit to Gradescope

Congratulations, you are finished with the mandatory portion of this lab!

Save your functions in a Python file named lab06.py and lab06_tests.py* in your directory **lab06. Then submit both files at the same time to Gradescope.

The following functions are optional extra-credit problems which should be submitted in a separate file lab06_bonus.py to a separate gradescope assignment lab06_bonus.

Encryption with a Binary Key

In this step we’ll introduce a variation to the Caesar cipher, resulting in a new cipher called the CS8 Cipher. It will be more secure since the offset defined by the key will still be constant, but sometimes the shift will be a forward shift and other times it will be a backward shift.

Whether the shift is forward or backward will be dictated by the binary representation of the key, which we will call the binary key. For example, a value of 2 is represented in binary as 10, i.e., two bits containing 1 followed by 0. At each step of the encryption, the algorithm will look at the next bit of the binary key. If it is 1, the shift will be forward, and if it is 0, the shift will be backward. After two characters, we will be at the end of the binary representation of the key, so we will need to start from the beginning of it.

Here are the new functions you will need to implement:

1) createBinKeyFromKey(key) - return binKey. Write a function that converts your key (which is an integer) to binary format (as a string of 0’s and 1’s). The built-in Python function bin takes an integer parameter and converts it to a binary string starting with 0b followed by the binary conversion. For example, bin(9) returns ‘0b1001’. Can you find a way to slice off the first two characters? (Hint: remember the slicing operator :.)

2) encryptCS8Cipher(plainText, key) - return cipherText. Now write a function that uses the same idea as the Caesar Cipher but instead of using the key by itself to find the character in the alphabet that will replace the current character, it will also use the binKey. The first few lines of this function need to:

• create your alphabet
• create binKey

To do these you will call the helper functions you created earlier. Then you will have to use a for loop to go through the characters of your plaintext and for each character you will have to perform the following procedure:

• Pick the next character of the binKey (if the length of the binKey is smaller than the length of the plainText, then you have to cycle back around from the beginning of binKey).
• If the character in binKey is ‘1’ then you will have to choose the character from the alphabet that is key positions forward in the alphabet. If the character in binKey is ‘0’ then you will have to choose the character from the alphabet that is key positions backward in the alphabet.

Here is a visualization of the encryption process:

Walk through it by hand to make sure you understand how it works.

3) decryptCS8Cipher(plainText, key) - return cipherText. Finally, write a function that will decrypt our CS8 Cipher. The procedure should be straightforward if you completed the previous part of the lab. Try to work out the solutions by hand first, if you are stuck.

4) Decode this message using key = 513 to verify that you are on the right track:

`#vyxACdjwk#pAjErCHdRWdCqrBdlxddnwCdrBdsljCdqnAndCfRvjtndCqnRZryqnACnGkRuxxtduxw-,AdjwmdlxfcnA`

Save your files and submit your work to Gradescope

Save your functions in a Python file named lab06_bonus.py in your directory lab06. Submit it to Gradescope in the assignment: lab06_bonus. (You will not get credit for it, if it is submitted under the regular assignment.)

Congratulations, you are finished with this lab!

Acknowledgments: Thanks to Ana Nika and Matthew Buoni for the initial version of this lab, and to Noah Stier and Jose Cuellar for adapting it for this assignment. Special thanks to Cindy Zhao, Olivia Gillam, and Sara Mandic for contributing warm-up functions.